Strahlungsquanten der Energie E = h • f besitzen einen Impuls von:
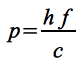Eq.20
Aus dem frontalen Auftreffen von n Strahlungsquanten pro Zeiteinheit auf eine Fläche A resultiert aus Gründen der Impulserhaltung eine Kraft F vom Betrag:
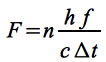
Der Ausdruck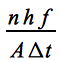
entspricht der lokalen Solarkonstante S [8], diese lässt sich nach dem Stefan-Boltzmannschen Strahlungsgesetz für einen Punkt im Abstand r aus der effektiven Temperatur der Sonne von ~5770 K und der Stefan-Boltzmann Konstante σ berechnen:
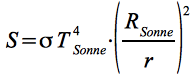
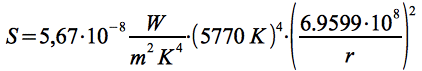Eq.20
Die wirkende Kraft ergibt sich demnach zu:
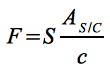Eq.21
Die Abb.6 b zeigt die Lage des Impulsvektors, der in einem Winkel α zur Normalen n der Fläche A treffenden Strahlung. Aus dem auf die Sonde übertragenen Impuls der absorbierten Strahlungsquanten folgt die Kraft F1. Wird die Strahlung zudem mit der Wahrscheinlichkeit r reflektiert, folgt eine zweite Kraft F2 entsprechender Größe.
Abb.6 a: Darstellung der auf die Fläche A auftreffende Sonnestrahlung.
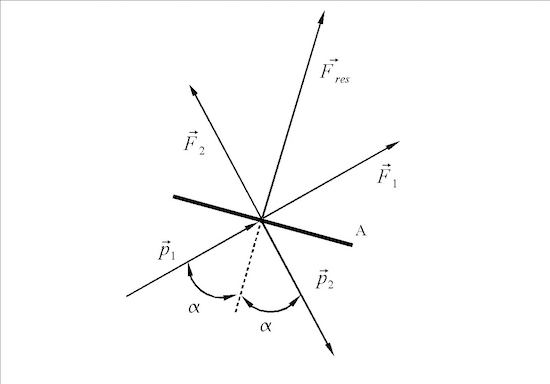
Abb.6 b: Darstellung der Impulsvektoren und den daraus resultierenden Kräften.
Im Falle einer hundertprozentigen Reflektion können die beiden Kräfte zu einer Resultierenden Fres in Richtung der Flächennormalen n zusammen gefasst werden. In vektorieller Schreibweise folgt demnach für F1:
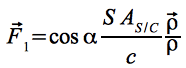Eq.22a
und für die resultierende Kraft Fres in Abhängigkeit von r:
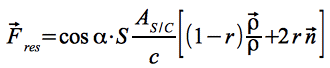Eq.22b
Der Winkel α zwischen der einfallenden Strahlung und der Flächennormalen n lässt sich berechnen aus:
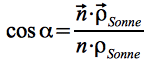Eq.23
Die Flächennormale des Satelliten sei immer in Richtung des Ortsvektors vom Planeten zur Sonde ausgerichtet, so dass gilt:
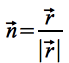
Durch Kenntnis des Winkels α lässt sich darüber hinaus bestimmen, ob der Satellit vom Planeten abgeschattet wird, so dass kein Strahlungsdruck auftreten kann. Unter Vernachlässigung von Dämmerungsphasen liegt Abschattung vor, wenn folgende Ungleichung erfüllt ist:
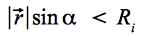Eq.24
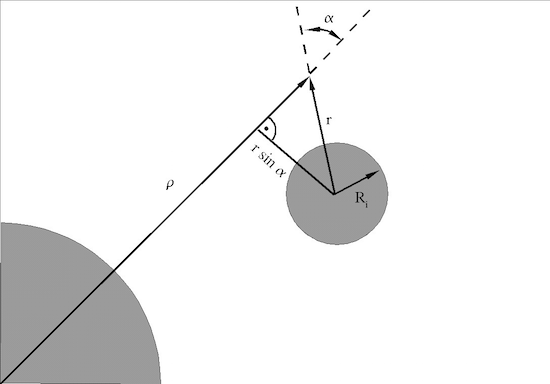
Abb.7: Darstellung der geometrischen Zusammenhänge zur Berechnung der Satellitenabschattung.
Neben der direkten Sonnenstrahlung ist auch die vom Planeten reflektierte Strahlung relevant und somit zu berücksichtigen. Im Zusammenhang mit dieser Albedostrahlung ist der Sichtfaktor zwischen Planet und Satellit von besonderer Bedeutung.
Der Sichtfaktor (view-factor) F12 zwischen dem Planeten mit der Flächen A1 und dem Satelliten mit der Fläche A2 gibt das Verhältnis der auf A2 treffenden zu der gesamten, von A1 emittierten Strahlung an und folgt allgemein aus [21]:
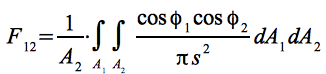Eq.25
Der Winkel φ1 wird eingeschlossen durch die Normale der Fläche dA1 und der Sichtlinie zwischen A1 und A2, der Winkel &phi2 entsprechend durch die Normale dA2 und der Sichtlinie (vergl. Abb.7 a).
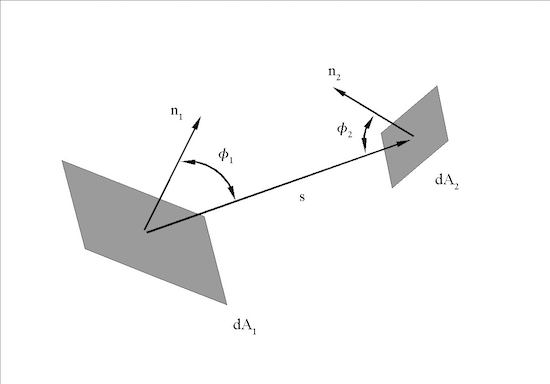
Abb.8 a: Darstellung der Flächenelemente dA1 und dA2.
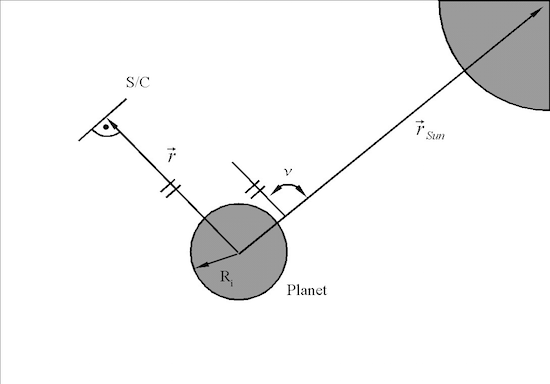
Abb.8 b: Darstellung des als flache Fläche modellierten Satelliten und der einfallenden Sonnenstrahlung.
Für einen als einfache Fläche modellierten Satelliten, dessen Fläche rechtwinklig zum Richtungsvektor vom Planeten zum Satelliten ausgerichtet ist, ergibt sich F12 zu (vergl. Abb.7 b):
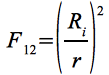Eq.26
Die Annahme aus Gl. Eq.26 ist zulässig, insofern gilt:
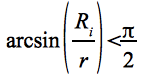
Die durch Albedostrahlung hervorgerufene Kraft berechnet sich somit zu:
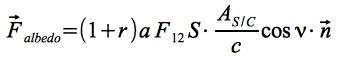Eq.27
In Gl. Eq.27 enthalten ist der vom Planeten abhängige Albedowert a (die Werte für Merkur und Venus sind angeben in Kapitel 2.1 und 2.2). Der Winkel ν folgt aus:
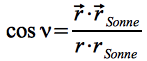Eq.28
Um ein Beispiel anzugeben, soll Falbedo für eine Sonde in 400 km Höhe über dem Merkur (a=0.056) abgeschätzt werden. Die Solarkonstante wird zu 14490 W m-2 angenommen, was dem Wert am Perihel des Planeten entspricht. Aus diesen Vorgaben ergibt sich ohne Reflektion (r=0) eine Kraft von 1.99785 • 10-6 N pro Quadratmeter.
Berücksichtigt man zudem die thermische Schwarzkörperstrahlung des Planeten, tritt eine dritte, durch Strahlungsdruck bewirkte Kraft auf:
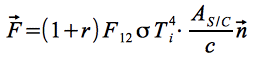Eq.29
Die Temperatur Ti ist hierbei die Schwarzkörpertemperatur der Planetenoberfläche. Für den Satelliten aus dem vorigen Beispiel folgt bei einer Schwarzkörpertemperatur von 442,5 K eine Kraft von 5.3523 • 10-6 N pro Quadratmeter.
Um die gesamten Störkräfte durch Strahlungsdruck zu berücksichtigen, müssen Eq.22, Eq.27 und Eq.29 aufaddiert werden.