Nachdem mit Eq.12 die Bewegung des Planeten in heliozentrischen Koordinaten beschrieben wird, soll nun die Bewegung der Sonde relativ zum Planeten untersucht werden. Ausgangspunkt ist hierbei, analog zu Eq.9, die Beschreibung der Bewegung in einem Inertialsystem, wobei in diesem Fall der Satellit als zehnte Größe hinzu kommt:
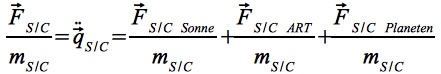
Eq.13
mit Eq.13 a:
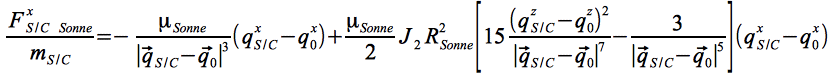
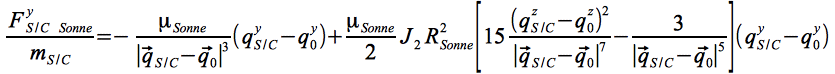
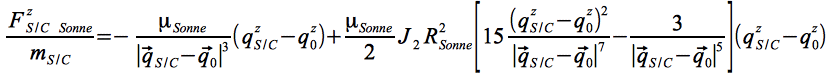
und:
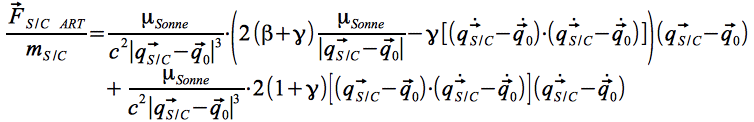Eq.13b
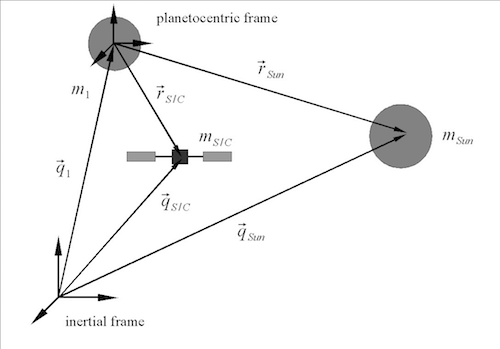
Abb.5: Lage von Sonne und Satellit in einem planeto-zentrischen Koordinatensystem (planetocentric frame).
An dieser Stelle sollen zudem noch die Einflüsse durch Inhomogenitäten im Gravitationsfeld des Planeten berücksichtigt werden, um den sich der Satellit bewegt. Das Gravitationspotential des entsprechenden Planeten (i) ist unter Berücksichtigung zonaler Terme darstellbar durch :
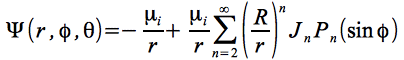Eq.14
Den entsprechenden Beitrag an der Bewegung des Satelliten erhält man durch:
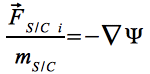Eq.15
In Komponentendarstellung und mit Berücksichtigung bis J2 hat Eq.15 die Gestalt:
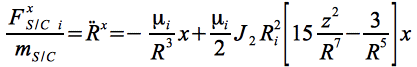Eq.15 a
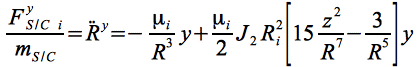
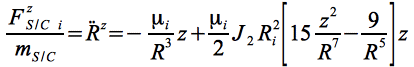
Eq.15 ist im Äquatorsystem des jeweiligen Planeten gegeben, das durch die Lage der Rotationsachse (Z-Achse) und der Knotenlinie aus Standarderdäquator und Planetenäquator (X-Achse) vorgegeben ist. Um die Darstellung im planetozentrischen Ekliptiksystem zu erhalten, sind folgende drei Drehungen nötig:
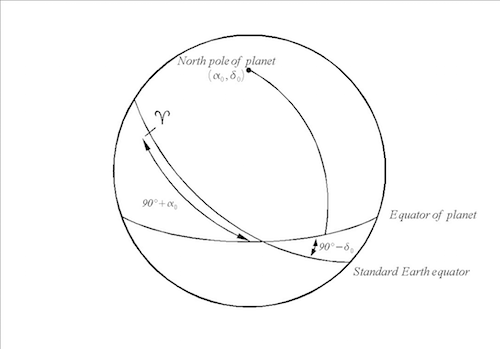
Abb.4: Beziehung zwischen Standarderdäquatorsystem und Äquatorsystem des Planeten.
Zunächst muss die Äquatorebene des Planeten durch eine Drehung um die Knotenlinie und um den Winkel 90°- σ0 in die Erdäquatorebene gedreht werden. Dies erfolgt durch Multiplikation mit:
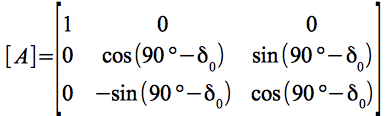
Anschließend wird die Knotenlinie (X-Achse) durch Drehung um die Normale des Erdäquators (Z-Achse) und um den Winkel 90°+ α0 auf den Frühlingspunkt ausgerichtet:
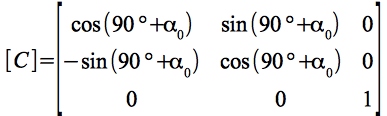
Die Darstellung im planetozentrischen Ekliptiksystem erfolgt letztlich durch Drehung der Erdäquatorebene in die Ekliptik:
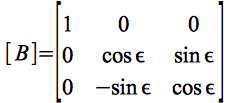
Der Winkel ε ist gegeben durch die Neigung der Äquatorebene zur Ekliptik (Im Fall der Erde ε ≈ 23.42°). Die vollständige Transformation von Eq.15 in das planetozentrischen Ekliptiksystem ergibt sich zu:
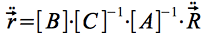Eq.16
Im Inertialsystem ist Eq.15 eine Funkti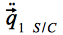on
von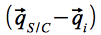 
und ersetzt in der Summenoperation den Term für j=i, so dass sich Eq.13 für einen Satelliten, der sich um den Planeten (i) bewegt, wie folgt schreiben lässt:
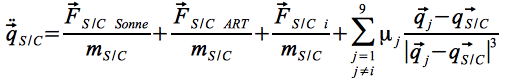Eq.17
Der Übergang in das planetozentrische Koordinatensystem erfolgt durch:
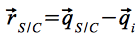
Somit ergibt sich die Bewegungsgleichung des Satelliten zu:
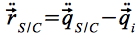
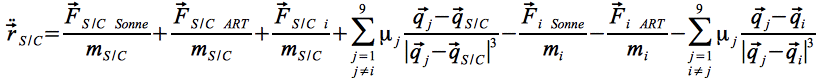Eq.18
Setzt man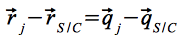
und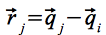 
ein und sortiert Eq.18 um, erhält man:
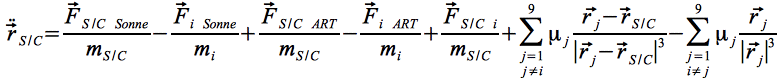
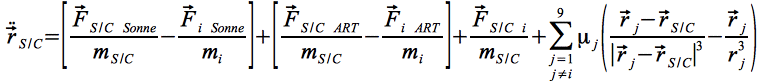Eq.19
mit den darin enthaltenen Ausdrücken Eq.19 a:
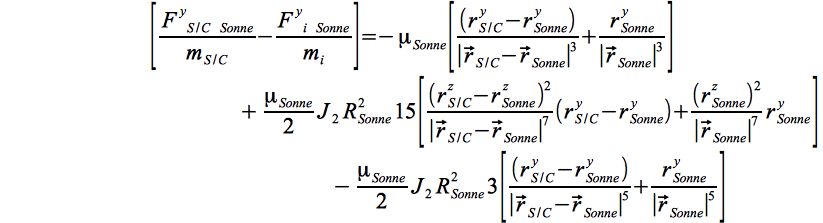
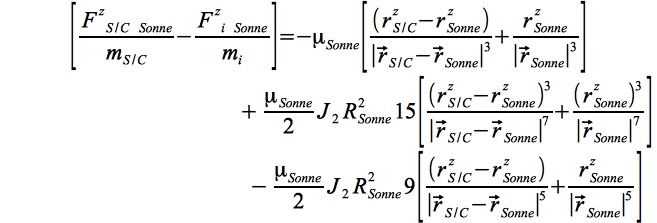
und Eq.19 b:
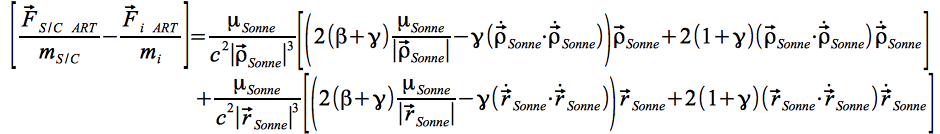
Mit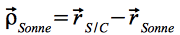
und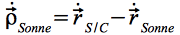 
.