Der wichtigste Effekt, auf dem die Radiosondierungsmessung beruht, ist der nach dem Physiker Christian Doppler (*29.11.1803, †17.03.1853) benannte Dopplereffekt. Von ihm 1842 entdeckt, bezog er sich ursprünglich auf die Änderung der Frequenz einer Schallwelle, die durch eine Relativbewegung zwischen Sender und Empfänger hervorgerufen wird. Nachgewiesen wurde der Dopplereffekt erstmals 1845 durch Buys-Ballot mit Hilfe zweier fahrender Eisenbahnzüge. Das Auftreten von Frequenzänderungen durch Relativgeschwindigkeiten und damit den Dopplereffekt bei elektromagnetischen Wellen beobachtete 1905 erstmals der Physiker Johannes Stark.
Der lineare Dopplereffekt stellt eine Näherungslösung des relativistischen Falles für kleine Geschwindigkeiten dar. Im folgenden soll er unter Berücksichtigung der Ausbreitung einer elektromagnetischen Welle in einem dispersiven Medium, wie dem interplanetaren Plasma, hergeleitet werden. Die Ausbreitungsgeschwindigkeit im Medium mit dem frequenzabhängigen Brechungsindex n ist gegeben durch:
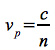Eq.35
wobei c die Ausbreitungsgeschwindigkeit im Vakuum darstellt. Der Brechungsindex selbst folgt aus:
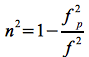Eq.36
Die hierin auftretende Plasmafrequenz fp ist von der Dichte der freien Elektronen im Medium abhängig und berechnet sich zu:
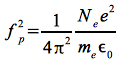Eq.37
(Die Größe Ne entspricht einer Elektronendichte mit der Einheit m-3.)
Aus Eq.36 wird deutlich, dass der Brechungsindex für Frequenzen unterhalb der Plasmafrequenz (f < fp) imaginär wird, was sich physikalisch darin äußert, dass keine Wellenausbereitung stattfindet. Statt dessen wird die EM-Welle nach einer von der Plasmafrequenz abhängigen Eindringtiefe („Plasma Skintiefe“) zurück gestrahlt [8]. In den hier diskutierten Anwendungen gilt jedoch immer f >> fp.
Nach Eq.35 ergibt sich im Plasma eine Phasenlaufzeitverzögerung Δ τpvon:
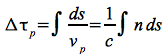Eq.38
Setzt man Eq.36 und Eq.37 ein folgt zwischen denn Punkten x1 und x2 entlang der Übertragungsstrecke s für die gesamte Phasenlaufzeit τp:
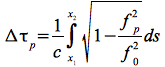
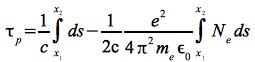
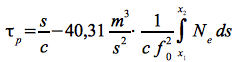Eq.39
Sendet ein Satellit ein Signal mit der Frequenz fT aus, berechnet sich die Phase ΦR des zum Zeitpunkt t von einer Bodenstation empfangenen Trägersignals (Einwegmodus) zu:
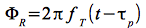
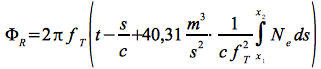Eq.40
Die gesuchte Frequenzverschiebung Δf = fT - fR folgt aus der zeitlichen Ableitung der Phase:
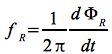
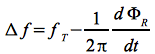
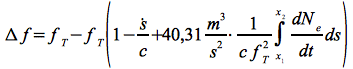
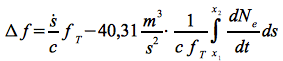Eq.41
Die Eq.41 beinhaltet den klassischen nichtrelativistischen Doppler-Effekt Δf1, der auf die Bahnbewegung zurück zuführen ist:
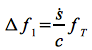Eq.42 a
sowie den von der zeitlichen Änderung der Elektronendichte abhängigen dispersiven Dopplereffekt Δf2:
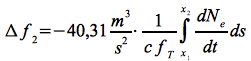Eq.42 b