Neben der bekannten Frequenzverschiebung durch eine Relativbewegung zwischen Sender und Empfänger sowie dem Durchlauf durch ein dispersives Medium ergibt sich auch eine Frequenzänderung zwischen zwei Punkten, die sich an unterschiedlichen Stellen in einem Gravitationsfeld befinden. Wie sich aus der Allgemeinen Relativitätstheorie ableiten lässt, hat das durch Masse hervorgerufene Potentialfeld Einfluss auf die „Ganggeschwindigkeit“ von Uhren. Der Potentialunterschied zwischen zwei Punkten bedeutet demnach einen „Gangunterschied“ zwischen sich dort befindlichen Uhren. Durch den unterschiedlich schnellen Ablauf der Zeit zwischen einer Sonde und einer erdgebundenen Bodenstation tritt eine zusätzliche Frequenzverschiebung auf:
Für das Eigenzeitintervall der Sonde gilt unter der Annahme, dass
das Gravitationsfeld schwach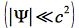 ist
[7]:
ist
[7]:
 Eq.43
Eq.43
Darin ist das aus der klassischen Mechanik bekannte Ψ bekannte negativ definierte Potential enthalten:
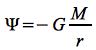 Eq.44
Eq.44
Anmerkung:In das lokale Gesamtpotential geht nicht nur das durch die Sonnenmasse hervorgerufene Potential ein, sondern auch das Gravitations- sowie das Rotationspotential eines Planeten.
Auf gleiche Weise, wie in Eq.43, gilt für die Bodenstation:
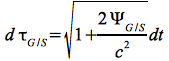 Eq.45
Eq.45
Die Koordinate t ist hierbei die Zeit eines nicht durch ein Gravitationsfeld beeinflussten äußeren Beobachters. Dieser Beobachter sieht in einem Zeitintervall Δt, dass zwei aufeinander folgende Wellenberge die Sonde verlassen und in einem gleichlangen Zeitintervall von der Bodenstation empfangen werden (One-way Downlink). Es gilt nun folgender Zusammenhang zwischen den Zeitintervallen und den Frequenzen des Signals an der Sonde (f0) und der Bodenstation (f1):
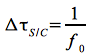 und
und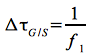
Es folgt nun unter Verwendung von Eq.43 und Eq.45:
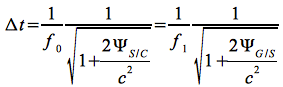
Demnach ergibt sich eine von der Bodenstation gemessene Frequenz f1:
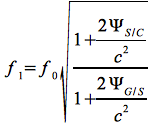 Eq.46
Eq.46
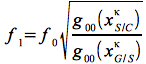
Die Größe g00 ist hierbei das Element i=0 und j=0 des metrischen Tensors gij [15].
Die mit z* bezeichnete Frequenzverschiebung bezogen auf die Sendefrequenz f0 folgt demnach zu:
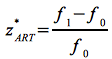
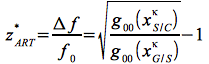 Eq.47
Eq.47
Die gesamte relative Frequenzverschiebung unter Berücksichtigung der Relativbewegung von Sender und Empfänger sowie der eben beschriebenen Gravitationsrotverschiebung führt auf folgende Beschreibung [23]:
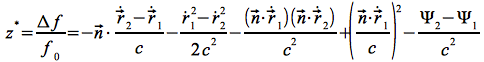 Eq.48
Eq.48
mit:
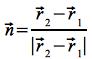
In Eq.48 treten die heliozentrischen Orts- und Geschwindigkeitsvektoren des Senders (1) und des Empfängers (2) auf. Es ist hierbei zu beachten, dass diese nicht zum gleichen Zeitpunkt gelten. Ein zum Zeitpunkt t0 abgestrahltes Signal benötigt eine Laufzeit Δt bis es den Empfänger erreicht, so dass das Signal erst zum Zeitpunkt t0+Δt empfangen wird.
Die Position und Geschwindigkeit der Bodenstation im heliozentrischen Ekliptiksystem erhält man durch:
Analog erhält man für den Satelliten:
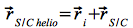 und
und 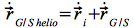 Eq.49b
Eq.49b
Mit Eq.48 lässt sich die Frequenzänderung für einen Signalweg bestimmen. Möchte man die relative Frequenzänderung auch unter Berücksichtigung einer Frequenzumsetzung k an Bord des Satelliten für einen Zweiwegemodus berechnen, gilt es, z*up und z*down aus den Positionen und Geschwindigkeiten von Satellit und Bodenstation unter Beachtung der Signallaufzeit zu bestimmen.
Die gesamte relative Frequenzverschiebung lässt sich nach folgender Überlegung recht einfach herleiten. Die Bodenstation sendet ein Signal mit der Frequenz f0, welches der Satellit mit der Frequenz f1 empfängt. Es gilt:
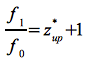
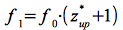 Eq.50
Eq.50
An Bord des Satelliten findet, bevor das Signal zurück gesendet wird, eine Frequenzumsetzung statt, so dass der Satellit mit der Frequenz f2 sendet. Es gilt für f2:
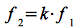 Eq.51
Eq.51
Die Bodenstation empfängt dieses Signal mit der Frequenz f3, dabei gilt:
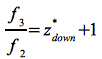
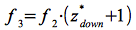 Eq.52
Eq.52
Setzt man Eq.50 in Eq.51 und diese in Eq.52 ein, erhält man:
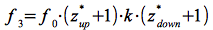
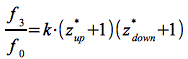
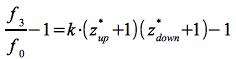
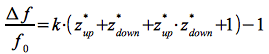
Die insgesamt auftretende Frequenzverschiebung z* ergibt sich demnach zu:
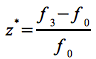
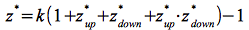 Eq.53
Eq.53
Differenziert man Eq.48 nach der Zeit, erhält man die relative Dopplerrate:
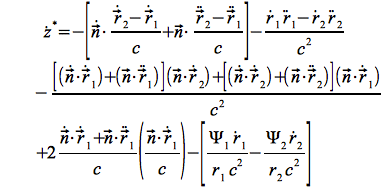 Eq.54
Eq.54
mit: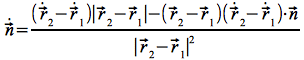
So dass für den Zweiwegemodus gilt:
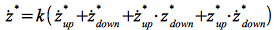 Eq.55
Eq.55
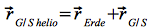 und
und 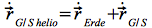 Eq.49a
Eq.49a